Bài toán
Cho $n$ hình chữ nhật trên mặt phẳng tọa độ, tính phần diện tích bị phủ bởi chính xác $2$ hình chữ nhật. Mọi phần diện tích bị phủ bởi $1$, hoặc $3$, hoặc $4$,… đều không được tính vào kết quả
Input
Dòng đầu tiên nhập số $n$
Từ dòng thứ hai trở đi, nhập $n$ dòng, mỗi dòng nhập $4$ số: $x_1, y_1, x_2, y_2$. Lần lượt thể hiện tọa độ góc trái dưới và phải trên của hình chữ nhật
Output
Một dòng duy nhất là phần diện tích bị phủ bởi chính xác $2$ hình chữ nhật
Giới hạn:
$1 <= n <= 10^5$
$-10^9 <= x_1 < x_2 <= 10^9$
$-10^9 <= y_1 < y_2 <= 10^9$
Test ví dụ
Input
3
1 3 4 5
3 1 7 4
5 3 8 6
Output
3
Minh họa
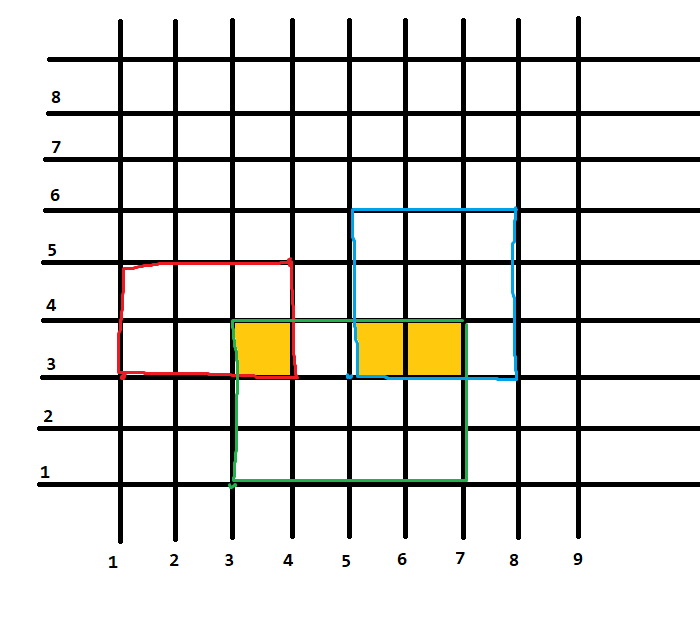
Lời giải
Có sự đóng góp lời giải cho hàm $\text{push_up()}$ đến từ ChatGPT
My comment: Rời rạc hóa dữ liệu, sort theo sự kiện x, update số lượng ô đang active trong quá trình sweepline thì mình có thể hiểu được
Còn logic về cây $\text{delta}$, để thể hiện số lượng đoạn con bị chồng lên tối thiểu thì mình không hiểu tại sao nó đúng.
Đoạn update cây $\text{T1}$, $\text{T2}$, $\text{T3}$ mình cũng không hiểu tại sao lại đúng luôn.
Nói chung là một bài yêu cầu logic rất cao
#include <bits/stdc++.h>
#define up(i,a,b) for (int i = (int)a; i <= (int)b; i++)
using namespace std;
const int maxn = 1e5 + 10;
const int MOD = 1e9 + 7;
struct EVENT{
int x;
int y1;
int y2;
int type;
};
//Các sự kiện sweepline gồm tọa độ x, độ dài y1, y2, và kiểu sự kiện
//đóng hay mở một đoạn thẳng
bool comp(EVENT& A, EVENT& B){
if (A.x == B.x) return A.type > B.type;
return A.x < B.x;
}
//Xử lý các sự kiện x trước
vector<EVENT> events;
vector<int> tempY;
int n, treesize;
long long T1[maxn << 3];
long long T2[maxn << 3];
long long T3[maxn << 3];
int delta[maxn << 3];
//treesize thể hiện kích thước thực sự của cây sau khi bị nén
//maxn << 1 cho số lượng sự kiện tối đa có thể xảy ra (1 mở và 1 đóng)
//maxn << 3 cho ước lượng segment tree trên toàn sự kiện
//T1 thể hiện segment tree quản lý diện tích bị phủ bởi ít nhất 1 đoạn thẳng
//T2: bị phủ bởi >= 2 đoạn thẳng
//T3: bị phủ bởi >= 3 đoạn thẳng
void push_up(int nod, int l, int r){
int len = tempY[r+1] - tempY[l];
if (delta[nod] >= 3) {
// đoạn này bị phủ >=3 lần => toàn bộ là T3
T3[nod] = T2[nod] = T1[nod] = len;
return;
}
if (l == r){
// Xử lý riêng các trường hợp nút lá
if (delta[nod] == 2) T1[nod] = T2[nod] = len, T3[nod] = 0;
else if (delta[nod] == 1) T1[nod] = len, T2[nod] = T3[nod] = 0;
else if (delta[nod] == 0) T1[nod] = T2[nod] = T3[nod] = 0;
return;
}
if (delta[nod] == 2){
// whole interval has +2; so >=1 and >=2 are full length
T1[nod] = T2[nod] = len;
// >=3 are positions where child had >=1
T3[nod] = T1[nod*2] + T1[nod*2+1];
return;
}
if (delta[nod] == 1){
// whole interval has +1 => >=1 is full length
T1[nod] = len;
// >=2 are positions where child had >=1
T2[nod] = T1[nod*2] + T1[nod*2+1];
// >=3 are positions where child had >=2
T3[nod] = T2[nod*2] + T2[nod*2+1];
return;
}
// delta == 0
T1[nod] = T1[nod*2] + T1[nod*2+1];
T2[nod] = T2[nod*2] + T2[nod*2+1];
T3[nod] = T3[nod*2] + T3[nod*2+1];
}
//Nếu "khoảng" [l, r] bị bao hoàn toàn thì lấy toàn bộ
//Nếu "khoảng" [l, r] chỉ bị bao một phần và không phải nút lá thì cập nhật dựa theo con
//Nếu "khoảng" lá không bị bao thì phải bằng 0
//Chú ý: nếu không có điều kiện (l != r) thì segment tree có thể lấy T[nod*2] với nod*2 là chỉ số tràn ngoài phạm vi đã khai báo
void update(int nod, int l, int r, int u, int v, int val){
if (r < u || l > v) return;
if (l >= u && r <= v){
delta[nod] += val;
push_up(nod, l, r);
return;
}
int mid = (l+r) >> 1;
update(nod*2, l, mid, u, v, val);
update(nod*2+1, mid+1, r, u, v, val);
push_up(nod, l, r);
}
signed main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
#define Task "A"
if (fopen(Task".inp", "r")){
freopen(Task".inp", "r", stdin);
freopen(Task".out", "w", stdout);
}
cin >> n;
up(i,1,n){
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
tempY.push_back(y1);
tempY.push_back(y2);
events.push_back({x1, y1, y2, 1});
events.push_back({x2, y1, y2, -1});
}
tempY.push_back(-MOD);
sort(tempY.begin(), tempY.end());
tempY.resize(unique(tempY.begin(), tempY.end()) - tempY.begin());
treesize = tempY.size()-1;
// tempY thêm phần tử -MOD để lấy lowerbound với chỉ số bắt đầu từ 1
// treesize = tempY.size()-1 vì phải bỏ qua phần tử -MOD;
sort(events.begin(), events.end(), comp);
long long res = 0;
for (int i = 0; i < (int)(events.size()-1); i++){
int u = lower_bound(tempY.begin(), tempY.end(), events[i].y1) - tempY.begin();
int v = lower_bound(tempY.begin(), tempY.end(), events[i].y2) - tempY.begin();
update(1, 1, treesize-1, u, v-1, events[i].type);
res += 1ll * (T2[1] - T3[1]) * (events[i+1].x - events[i].x);
// Segment tree quản lý các "khoảng" giữa tọa độ điểm này và tọa độ điểm kia
// có treesize tọa độ điểm thì có treesize-1 "khoảng"
// Tại mỗi nút chỉ số v quản lý khoảng [l, r], lấy kết quả nút nếu bị bao toàn bộ là tempY[r+1] - tempY[l]
// Do đó, mỗi lần lấy kết quả trong tọa độ [u, v] thì lấy kết quả trên "khoảng" [u, v-1] trên segment tree
// cout << T1[1] << " " << T2[1] << " " << T3[1] << " " << res << " ";
// cout << u << " " << v << "\n";
}
cout << res;
}
Bonus
test tính năng gõ MathJax v3
\[K(a,b) = \int \mathcal{D}x(t) \exp(2\pi i S[x]/\hbar)\]